This quarter I’m taking a course called “Algebraic Analysis”. It’s being taught by Carl Mautner, who does rep theory and algebraic geometry here at UCR. I’ve had a bunch of classes with him before, and they were always fun. These are the notes from the first class. It was sort of running through the motivation from analysis, plus an overview of the rest of the quarter. He said this is the first and last time we were going to do analysis in this class.
What is Algebraic Analysis?
“analysis using ring theory and homological algebra”
Suppose we want to study a linear PDE on an open subset of
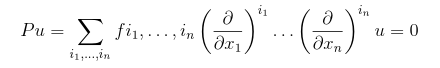
here u is some unknown function, f analytic on X. P is an element of D, the (non-commutative) ring of differential operators on X.
Let be the commutative ring of analytic functions on X. Then
is naturally a left D-module, where D acts by differentiation.
Saito: Associate to the PDE Pu=0 the left D-module M := D/DP. Then
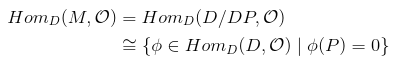
Note: by
is an isomorphism. Then under this identification
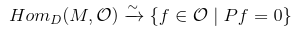
because . Hence
is the group of holomorphism solutions to our PDE!
Note: the same is true if we replace $\mathcal O$ with any other flavor of functions that admit a natural action of D, e.g. smooth functions or Schwartz distributions.
More generally, given a system of linear PDE’s of n unknown functions :
for i=1,…,k, . Consider the left D-module M defined as the cokernel:
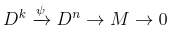
where . Then similar to before, we have
is the space of solutions to the family of equations.
So studying linear PDE’s is equivalent to studying the functor from the category of left D-modules admiting finite presentation to the category
.
Equations can have local solutions that don’t extend… so we study sheaves. Instead of , we study
sheaf of functions, and instead of D, we study
sheaf of diff ops.
Our main objects of study then become left D_x-modules, i.e. coherent D_x-modules, and the functor sending left coherent D_x modules to
.
Remark: We can let X be any complex manifold.
The space of holomorphic solutions to any ODE is finite dimensional. In order to get finite dimensionality in higher dimensions, we have to restrict to a “nice” class of D_x-modules, called holonomic.
In ODE’s, one has a good class of equations that have “mild singularities”, called regular singularities. By analogy, one defines regular holonomic D_x-modules. The functor is not exact, so we want to study derived functors
.
So really in this class we’ll study restricted to regular holonomic D_x-modules, mapping into
.
Theorem [Riemann-Hilbert]
This functor is fully faithful and it has essential image in , an abelian category called the category of perverse sheaves.
Connection to Representation Theory
Let G be a semisimple -algebraic group (e.g. SL_n, SO_n, Sp_n, … , E_8), let
.
Question [Verma]: how can we determine the characters of infinite dimensional highest weight modules of ?
[Kazhdan-Lusztig]: conjecture answer in terms of geometry of Schubert varieties, flag varieties, G/B where B is the Borel subgroup (sorry the notes get a little fuzzy here). Key idea: G acts on G/B, which gives , which gives
.
So, given a -module, we get a
-module! This gives an action of
on
.
[Beilinson-Bernstein]: This is an equivalence of categories
[KL]: Use this bridge to apply a deep theorem about perverse sheaves, the decomposition theorem of BBDG to prove the conjecture.
Outline of the Course
- some theorems about smooth manifolds and smooth complex algebraic varieties
- sheaves & derived categories
- intersection cohomology
- perverse sheaves
One thought on “Algebraic Analysis notes Lecture 1 (7 Jan 2019)”