Algebraic Analysis notes Lecture 2 (9 Jan 2019)

Lecture 1 notes here.

Recall that in algebraic topology, we construct homotopy invariants, e.g. homology. Homology measures “global” topology, but its not very sensitive to local structure.

However, Poincare noticed that if X is a closed oriented manifold of real dimension n, then $dim H_k(X, \mathbb R) = dim H_{n-k} (X, \mathbb R)$ .

Poincare Duality: Let X be an orientable manifold of dimension n. Then there exists natural isomorphisms
$[X] \cap - \colon H_K(X, \mathbb Z) \rightarrow H_c^{n-k} (X, \mathbb Z)$
where [X] is the fundamental class.

Theorem: Let X be a smooth complex affine variety of complex dimension n. Then X has homotopy type of a CW complex of real dimension n. In particular, $H_k(X, \mathbb Z) = 0$ for k>n.

Proof idea: Morse Theory

Definition: Let X be a manifold. A smooth function $f \colon X \rightarrow \mathbb R$ is Morse if

for any real number s, $f^{-1}((-\infty, s]) \subseteq X$ is compact,
every critical point of f is non-degenerate

Recall, a point x in X is a critical point of f if $df \mid_x = 0$ , and a critical point is non-degenerate if the Hessian (symmetric bilinear form on $T_x X$ defined by second partials) is non-degenerate. The index of a non-degenerate critical point is the number of negative eigenvalues of the Hessian.

Example: consider the “height” function on an upright torus,

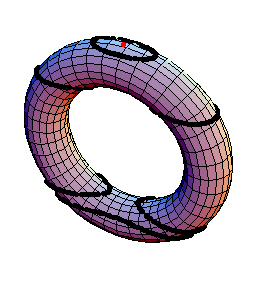
image taken from: https://www.mimuw.edu.pl/~akoz/Mathematica/IMS2001/Morse/index.html

it has four critical points, depicted below

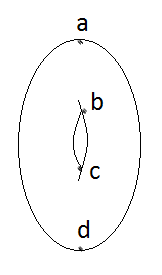
image taken from https://faculty.math.illinois.edu/~ruiloja/Math519/lanius.pdf

Note that d has index 0, c has index 1, b has index 1, and a has index 2.

Theorem: Let $f \colon X \rightarrow \mathbb R$ be a Morse function. Then X has the homotopy type of a CW complex with one cell for each critical point, and each cell has dimension equal to the index of the corresponding critical point.

So in the torus example, you think of building the CW complex by starting at the bottom, you start with a 0-cell. As you scan up, you have a disk, which is still homotopic to a point. Then when you reach c, you have to introduce a 1-cell, and it something like a basket with a handle. Then when you reach b, you have to add another 1-cell, and at a you add the 2-cell. This will give you a CW complex that looks like the standard way to build a torus by identifying sides of a square.

Lemma: Let $X \subset \mathbb R^N$ be a manifold. For y in $\mathbb R^N$ , the function $f_y \colon X \to \mathbb R$ given by sending a point x to $||x-y||^2$ is Morse.

proof: Note $df_y |_x (u) = 2<x-y, u>$ For any tangent vector u in $T_x X$ . So x is a critical point of $f_y$ iff x-y is perpendicular to $T_x X$ . Let $Z = \{(x,y) \in X \times \mathbb R^N \mid x-y \bot T_x X\}$ . Let $p \colon Z \rightarrow X$ and $q \colon Z \rightarrow \mathbb R^N$ be the projection maps. Note: p realizes Z as the orthogonal complement to the bundle TX in $T \mathbb R^N|_x$ . Then dim Z = n + N – n = N. Now consider $q \colon Z \rightarrow \mathbb R^N$ , and notice the domain and codomain have the same dimension. q is submersive at (x,y) iff q is immersive at (x,y).

claim: q is immersive at (x,y) in Z iff the critical point x of $f_y$ is non-degenerate.

proof: q is immersive at (x,y) iff for any $u \in T_x X$ , $(u,0) \notin T_{(x,y)} Z$ . We can express Z as the zero-set of

$\sigma \colon X \times \mathbb R^N \rightarrow p^* T^* X$
$(x,y) \mapsto (TX \rightarrow \mathbb R)$
$u \mapsto df_y(x)(u) = 2<x-y, u>$

In local coordinates {x_i} on X near x,

$\sigma(x,y) = \sum^n \frac{\partial f_y}{\partial x_i}|_x dx_i$

Let $\{y_\alpha\}_{\alpha =1}^N$ be coordinates on $\mathbb R^N$. For $u \in T_xX$ and $v \in T_y \mathbb R^N$ , let $u = \sum^n u_i \frac{\partial}{\partial x_i}$ , and $v = \sum^N v_\alpha \frac{\partial}{\partial y_\alpha}$ .

$(u,v) \in T_{(x,y)} Z \Leftrightarrow 0 = (d\sigma(u,v))_i = \sum_j u_j \frac{\partial^2 f_y}{\partial x_j \partial x_i} +\sum_\alpha v_\alpha \frac{\partial^2f_y}{\partial y_\alpha \partial x_i}$

which gives

$(u,0) \in T_{(x,y)} Z \Leftrightarrow 0 = \sum_j u_j \frac{\partial^2 f_y}{\partial x_j \partial x_i}$ , and this somehow gives what we wanted.

Lemma: For $X \subseteq \mathbb C^n$ smooth algebraic variety and $f_y \colon X \rightarrow \mathbb R$ defined by the standard Euclidean scalar product on $\mathbb C^n$ , the index of $f_y$ is less than or equal to n at every critical point.