Algebraic Analysis notes Lecture 3 (11 Jan 2019)

Notes for Lecture 2

Theorem: If $X \subset \mathbb C^N$ is a smooth affine complex algebraic variety of complex dimension n, then X has the homotopy type of a CW complex of real dimension n.

Note that this theorem is saying that certain spaces of real dimension 2n are homotopic to spaces with half the dimension.

Last time we showed that for generic y in $\mathbb C^n$ , $f_y \colon X \to \mathbb R$ given by $x \mapsto ||x-y||^2$ is Morse! In particular, it has non-degenerate critical points. So X has the homotopy type of a CW complex with one cell for each critical point x of $f_y$ which will have dimension equal to the index of the critical point. We want to show that at any critical point, the index is at most n. We computed for $u,v \in T_xX$

$Hess_x f_y(u,v) = 2(<u,v>_\mathbb R + <x-y, \nabla_v u>_\mathbb R)$

Let $Q(u,v) = <x-y, \nabla_v u>_\mathbb R$ .

claim: Q is the real part of a complex bilinear form H on $T_xX \cong \mathbb C^n$ .

Assume for a moment that this claim is true. Consider the map given by multiplication by i on $T_xX$ , $i- \colon T_xX \rightarrow T_xX$ . This is unitary with respect to the standard Hermitian form $<-,->_\mathbb C$ . So $H(iu,iv) = -H(u,v)$ , and then $Q(iu, iv) = -Q(u,v)$ . If $\{u_k\}$ is an orthonormal eigenbasis with eigenvalues $\{\lambda_i\}$ , then $\{i u_k\}$ is also an orthonormal eigenbasis, but now with eigenvalues $\{-\lambda_i\}$ . So Q has eigenvalues in pairs $\{\pm \lambda_i\}$ , so Hess_x has eigenvalues $\{2 (1 \pm \lambda_i)\}$ . At most one of these is negative, so Hess_x has at most n negative eigenvalues. So the index of x is less than or equal to n, as desired.

Sketch of proof for the claim:

$Q(u,v) = <x-y, \nabla_v u>_\mathbb R = Re <x-y, \nabla_v,u>_\mathbb C$
$re <x-y, \mathbb I (u,v)>_\mathbb C$

where $\mathbb I \colon T_xX \times T_xX \rightarrow \mathbb C^n / T_xX$ is given by $(u,v) \mapsto \pi (\nabla_v u)$ , where $\pi \colon \mathbb C^n \rightarrow \mathbb C^n/ T_x X$ .

Now, $\mathbb I$ can be recognized as the derivative of a complex algebraic map. Let $\nu \colon X \rightarrow Gr^\mathbb C(n,N)$ (where $Gr^\mathbb C(n,N)$ is the Grassmannian of n-planes in N-space) given by $x \mapsto T_x X \subset \mathbb C^N$ . Then $d\nu \colon T_xX \to T_{T_xX} Gr(n,N) = Hom_\mathbb C(T_xX, \mathbb C^N/T_xX)$ . Which gives a map (via currying, if you saw Jade’s tweet) $\mathbb I \colon T_x X \times T_x X \to \mathbb C^N/T_xX$ . Since $d\nu$ is linear, then $\mathbb I$ is bilinear, as $<-,->_\mathbb C$ is linear in the second entry.

This proves the theorem, which is the starting point for a lot of cool stuff.

Lefschetz Hyperplane Theorem: Let $X^n \subset \mathbb P^N$ be a complex projective (possibly singular) variety, and $H \subset \mathbb P^N$ be a hyperplane. Let $Y = X \cap H$ . Assume that X\Y is smooth. Then $H^k (X, Y; \mathbb Z) = 0$ for k≤n-1. In particular, $i \colon Y \hookrightarrow X$ induces the map $i^* \colon H^k(X) \to H^k(Y)$ , which is an isomorphism for k<n-1, and injective for k=n-1.

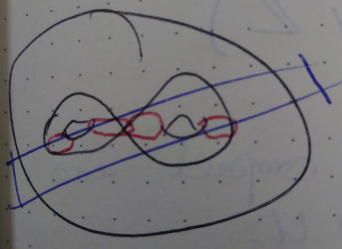
In the picture, the black circle is the ambient projective space, the black torusy thing is the variety X, the blue rectangle is the hyperplane, and the red bits are the intersection Y.

proof: Let U=X\Y. Note, if you remove a hyperplane from projective space, you gen an affine space, so U is a smooth affine variety! Choose a fundamental system of neighborhoods ${Y_i}$ of Y such that $Y_i$ deformation retracts onto Y for any i. Note that $X \setminus Y_i \subset U$ is compact and is a deformation retract of an open set in U. Then

$H^k (X, Y; \mathbb Z) \cong \varinjlim H^k (X, Y_i; \mathbb Z)$
$\cong \varinjlim H^k(U, U \cap Y; \mathbb Z)$ by excision
$\cong \varinjlim H^k_c (X\ Y_i; \mathbb Z)$
$\cong \varinjlim H_{2n-k} (X \setminus Y_i; \mathbb Z)$ by Poincare duality
$\cong H_{2n-k} (U; \mathbb Z) = 0$