Algebraic Analysis notes Lecture 4 (14 Jan 2019)

Posted byJoe MoellerPosted inAlgebraic Geometry

Notes for Lecture 3

Last time, we proved the Lefschetz hyperplane theorem.

Lefschetz Hyperplane Theorem: Let X^n \subset \mathbb P^N be a projective variety and H \subset \mathbb P^N a hyperplane such that U= X \setminus Y (where Y = X \cap H) is smooth. Then H^k (X, Y; \mathbb Z) = 0 for k≤n-1. (Equivalently, i^* \colon H^*(X) \rightarrow H^*(Y) is an isomorphism for k<n-1, and an injection for k= n-1.

Today we will see an example of how to use this theorem.

Let Z \subset \mathbb P^n be a degree d hyperplane. Then Z is the intersection of a hyperplane in H\subset \mathbb P^N with the image of \mathbb P^n under the degree d Veronese embedding (\mathbb P(V) \rightarrow \mathbb P(Sym^d V))

Apply Leftschetz hyperplane theorem with X = \mathbb P^n and Y = X \cap H = Z. We get i^* \colon H^k (\mathbb P^n) \rightarrow H^k (Z) is an isomorphism for k<n-1, and an injection for k=n-1.

Recall H^k (\mathbb P^n; \mathbb Z) = \mathbb Z [\alpha] / \alpha^{n+1} where \alpha is degree 2.

If Z is smooth, then by Poincare Duality (and universal coefficients theorem), for n-1<k ≤2n-2, H^k(Z, \mathbb Z) \cong H^{2n-2-k} (Z)^*, which is \mathbb Z when k is even and 0 when k is odd.

Let’s go back to X \subset \mathbb P^N smooth projective, and Y= X\cap H. To start, suppose that Y is smooth. Then the composite of

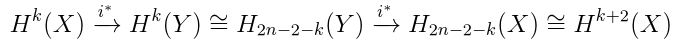
gives an operator on homology which raises the degree by 2. More generally, if X \subset \mathbb P^N projective, consider - \cup j^*(PD[H]) \colon H^k (X) \rightarrow H^{k+2} (X) Call this the “Lefschetz operator”, call it \eta. Turns out this is the same operator as the composite above.

Hard Lefschetz Theorem: Let X be a smooth projective variety of dimension n. For any embedding X \subset \mathbb P^N and 0≤i≤n, \eta^i \colon H^{n-i} (X; \mathbb Q) \rightarrow H^{n+i} (X; \mathbb Q) is an isomorphism!

Notice: rational coefficients. Also, by Poincare Duality, we already knew dim H^{n-i} (X; \mathbb Q) = dim H^{n+i} (X; \mathbb Q), so the juice of the theorem is really that we have a specific isomorphism.

Historical note: We’ll skip the proof, it is hard after all. Grothendieck named the theorem. It was originally proven by Lefschetz in 1924, but nobody could really follow the proof. A better proof was later given by Hodge in 1941, using Hodge theory. Grothendieck and his school later created a cohomology theory for varieties and proved this using ideas similar to those presented by Lefschetz.

Corollary: The map \eta \colon H^k (X; \mathbb Q) \to H^{k+2} (X; \mathbb Q) is injective for k<n, and surjective for k ≥ n. Hence the even (resp odd) Betti numbers b_k = dim_\mathbb Q H^k (X; \mathbb Q) grows as k gets closer to n.

Definition: Say \alpha \in H^{n-i} (X; \mathbb Q) is primitive if \eta^{i+1} \alpha = 0. Let H^k_{prim} (X; \mathbb Q) = \{ \alpha \in H^k (X;Q) |\alpha \text{ is primitive} \}

Corollary: Every $\alpha \in H^k (X; \mathbb Q )$ admits a unique decomposition $\alpha = \sum_r \eta^r \alpha_r$ where $\alpha_r \in H^{k-2r}_{prim} (X; \mathbb Q)$. So H^k (X; \mathbb Q) = \bigoplus_{2r \leq k} \eta^r H^{k-2r}_{prim} (X; \mathbb Q).

Finer structure: Poincare Duality gives P \colon H^k (X; \mathbb Q) \times H^{2n-k} (X; \mathbb Q) \rightarrow \mathbb Q given by (\alpha, \beta) \mapsto [X] \cap (\alpha \cup \beta). P is nondegenerate. With hard Lefschetz, this gives a nondegenerate bilinear form on H^k(X; \mathbb Q); for \alpha, \beta \in H^k (X; \mathbb Q), Q(\alpha, \beta) = P (\eta^{n-k} \alpha, \beta) = [X] \cap (\eta^{n-k} \cup \alpha \cup \beta).

Note when k is even Q is symmetric, when k is odd Q is antisymmetric.

On H^k (X; \mathbb C) define \mathbb H_k (\alpha, \beta) = i^k Q(\alpha, \overline{\beta}) defines a Hermitian form.

Lemma: The Lefschetz  decomposition H^k (X; \mathbb C) = \bigoplus_{2r \leq k} \eta^r H^{k-2r}_{prim} (X; \mathbb C) is orthogonal with respect to \mathbb H_k.

Notes for Lecture 5

Published by Joe Moeller

Mathematician

2 thoughts on “Algebraic Analysis notes Lecture 4 (14 Jan 2019)”

  1. Pingback: Algebraic Analysis notes Lecture 3 (11 Jan 2019) – Joe Moeller
  2. Pingback: Algebraic Analysis notes Lecture 5 (16 Jan 2019) – Joe Moeller

Leave a comment