Last time, for a given topological space X and a ring k, we define a presheaf to be a functor .
Definition: If F is a presheaf on X, and x is a point in X, then the stalk of F at x, is the k-module .
Let’s unpack this: an element of is an equivalence class of pairs (U, s) where U is an open neighborhood of x, and
, and
if there is a set V contained in
such that
, a “common refinement”.
If , there is a canonical map
, and the image of a section
under this map is called the germ of s at x, denoted
.
Definition: Let , the support of F is
. For
, let
.
Exercise: supp(s) is always closed (that’s why the definition doesn’t have to include taking the closure).
Definition: A presheaf F on X is a sheaf if it satisfies the following:
(S1) Gluing: given an open cover of U open in X, and
such that
, then there exists
such that
.
(S2) Local Identity: given an open cover of U open in X, and
such that
, then s=t.
We’re thinking of F(U) as the set of functions from U into k. So the first condition (S1) is saying that if we have a cover of U by open sets, and we have a function on each of these opens, and they all agree on overlaps, then we can glue them all together into a function on all of U. The second condition (S2) says that if two sections agree for any restriction to a set in the open cover, then they must be equal. Taken together, if you have two candidates for what the gluing of a compatible family of sections could be, they must be equal, i.e. they glue to a unique section s on U.
A morphism of sheaves is just a morphism of presheaves. So the category of sheaves on X is the full subcategory of PreSh(X).
Notice that if F is a sheaf, then the local identity condition gives . If F is a sheaf, and
is an oper cover of U, we get a sequence
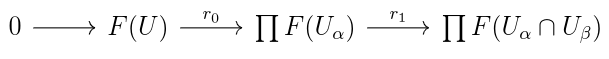
where is given by
, and
is given by
. F being a presheaf gives that
. The gluing condition gives that
. The local identity condition gives that
is injective. Thus if F is a sheaf, then this sequence is exact.
Lemma: Let . The following are equivalent:
- F satisfies local identity (S2)
- for any U open in X, and
, if
for any point x in U, then s = 0.
- for any U open in X, and
, if
for each point x in U, then s = t.
proof: (1 implies 2) Suppose and
for each x in U. Then for each x in U, there is a neighborhood
of x such that
. So we have an open cover
of U, and
, so local identity gives s=0.
(2 implies 3) Suppose we have with
for each point x in U. Then if we consider s-t, it reduces to the statement of 2.
(3 implies 1) Suppose (S2) fails. Then there is some U open in X, and some , and some open cover
such that
for every
. Then the germs of s and t agree,
, and thus s=t by 3. Contradiction!
Conclusion: any sheaf can be recovered from the germs of its sections!
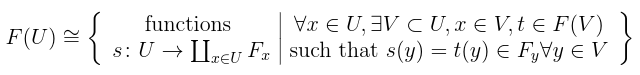
Example: First a non-example. The constant presheaf is usually not a sheaf because
which is required to be trivial.
Definition: The constant sheaf, denoted or
when the space is clear, is given by
, and
is just given by restriction of functions.
More generally, for all closed, we write
or just
for
.
For example, if X is Hausdorff, then for a point x in X, {x} is a closed subset, so then is M if x is in U, and 0 otherwise.
Next time: Sheafification.
2 thoughts on “Algebraic Analysis notes Lecture 6 (18 Jan 2019)”