Algebraic Analysis notes Lecture 7 (25 Jan 2019)

Posted byJoe MoellerPosted inAlgebraic Geometry

Notes for lecture 6

Sheafification

Last time: for a space X and a ring k, a presheaf is a functor Op(X)^{op} \to k-mod, and a sheaf is a presheaf F such that for any open U in X and any open cover (U_\alpha)_{\alpha \in I} of U, the sequence

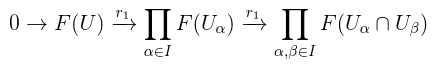
is exact.

If we let X=*, then the functor Sh(X; k) \to k-mod is an equivalence. Note this isn’t true for presheaves because you also have to assign the empty set to something as well.

Examples:

  • Constant sheaf \underline M_X
  • For a point x in X, the “skyscraper sheaf” at x \underline M_x
  • The sheaf of functions on X, denoted \mathcal O_X, defined by \mathcal O_X(U) = \{ f:U \to k\}. This is a sheaf because functions glue in an obvious way
  • If p: E \to B is a k-vector bundle, then we get a sheaf of sections: for open subset U of B, let \Gamma (U) = \{ \text{sections } s \colon U \to E \mid p \circ s = id_U \}.

In fact, we saw previously that an sheaf can be thought of as a sheaf of sections for some bundle-like object

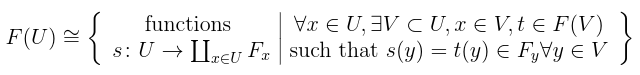
Following this idea:

Proposition: For any presheaf F on X, there is a sheaf F^+ and a morphism i \colon F \to F^+ such that for any sheaf G on X and morphism \phi \colon F \to G there is a unique map \phi^+ \colon F^+ \to G such that \phi = \phi^+ \circ i.

F^+ is called the sheafification of the presheaf F.

Sketch of proof: We’ll turn the big weird equation before the proposition into a definition. Define:

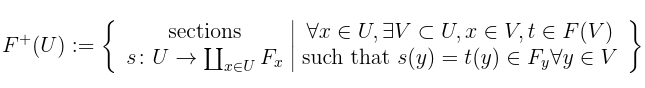
Note that if t \in F(U), let i_U(t) \colon U \to \coprod_{x \in U} F_x by x \mapsto t_x \in F_x. This defines our map i \colon F \to F^+. Remains to check the universal property.

Given a sheaf G on X, and \phi \colon F \to G, we want to define \phi^+ \colon F^+ \to G. Consider U open in X, and s \in F^+(U). Choose an open cover (V_\alpha)_{\alpha in I} of U, and for each \alpha choose a section t_\alpha \in F(V_\alpha) such that s(y) = t_y for each y in V_\alpha. Then \phi_{V_\alpha}(t_\alpha)|_{V_\alpha \cap V_\beta} = \phi_{V_\alpha}(t_\beta)|_{V_\alpha \cap V_\beta} because the germs of both sides at y \in V_\alpha \cap V_\beta are \phi_y(s(y)). But G is a sheaf, so the \phi_{V_\alpha} (t_\alpha) glue to give a unique element u \in G(U). Let \phi^+_U(s)=u.

To summarize: the map i \colon F \to F^+ induces isomorphism

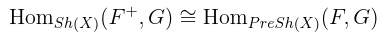
This says that sheafification is a left adjoint to the forgetful functor Sh(X) \hookrightarrow PreSh(X).

Abelian Categories

We’re going to show Sh(X;k) is an abelian category so we can use homological algebra!

Definition: A category C is additive if
(A1) for object X and Y in C, \mathrm{Hom}_C (X, Y) is an abelian group, and composition \mathrm{Hom}_C (X, Y) \times \mathrm{Hom}_C (Y, Z) \to \mathrm{Hom}_C (X, Z) is a group homomorphism
(A2) there is a zero object, 0 in C, such that \mathrm{Hom}_C (0, 0) = \{0\} (exercise: this is equivalent to saying that 0 is initial and terminal in C)
(A3) C has biproducts, called direct sum

Examples of additive categories:

  • the category of abelian groups, Ab
  • PreSh(X;k)
  • Sh(X;k)

Definition: Let \phi \colon X \to Y be a morphism. We say that \phi has kernel ker \phi \in ob(C) if there is a morphism k \colon ker \phi \to X such that \phi \circ k = 0, and for any k' \colon A \to X such that \phi \circ k' = 0, then there is a unique h \colon A \to ker \phi such that k' = k \circ h.

Example: Let F and G be sheaves on X, and \phi \colon F \to G. Let ker \phi (U) = ker(\phi_U \colon F(U) \to G(U)). Check that ker \phi is a sheaf on X and is indeed the kernel of \phi in the category Sh(X).

We’ll continue with abelian categories next time.

Notes for Lecture 8

Published by Joe Moeller

Mathematician

2 thoughts on “Algebraic Analysis notes Lecture 7 (25 Jan 2019)”

  1. Pingback: Algebraic Analysis notes Lecture 6 (18 Jan 2019) – Joe Moeller
  2. Pingback: Algebraic Analysis notes Lecture 8 (28 Jan 2019) – Joe Moeller

Leave a comment