Combinatorics, Lecture 5 (10 October 2019)

Thanks to Tim Hosgood for helping me type these notes up.
Previous lecture here.

Fibonacci and `tribonacci’ numbers

Recall: there’s a species $G \colon \mathsf S \to \mathsf F$ with

G(X) = {ways to totally order X and chop it into blocks of length 1 or 2}

For example,

We saw that

$|G|(X) = \sum_{n\geq0} \frac{ |G(n)|}{n!} x^n = \sum_{n\geq0} F_n x^n$

where $F_n$ is the n-th Fibonacci number. Note that $n!F_n=|G(n)|$ ; it’s not $F_n=|G(n)|$ . We also saw that $|G|(X)= \frac{1}{1-x-x^2}$ which implies that $|G|(X)= 1 + X|G|(X) + X^2|G|(X)$ . This would follow from $G \cong Q_0 + Q_1 G + Q_2 G$ if $Q_k$ were a species with $|Q_k| (X) = x^k$ . Before, we talked about $A_k$ as the species of “being a k-element set”, with

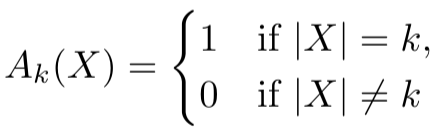
but this gives that $|A_k|(X)=x^k/k!$ . What we now want is $Q_k$ , the species of “being a totally-ordered k-element set”, with

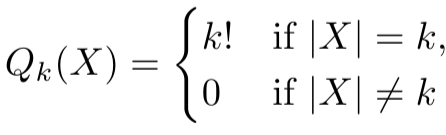
so that $|Q_k|(X)= \sum_{n\geq0} \frac{|Q_k(n)|}{n!} n! = x^k$ .

To totally order X and chop it into blocks of length 1 or 2, you just

see if $X=\emptyset$ , and stop if so; otherwise
chop X into two subsets: the first with 1 element, and the second totally ordered and chopped into blocks of length 1 or 2; or
chop X into two subsets: the first with 2 elements, and the second totally ordered and chopped into blocks of length 1 or 2.

Note that $TO \cong A_0 + A_1 TO \cong Q_0 + Q_1 TO$ gave us $|TO|(X) = \frac{1}{1-x}$ . Going one level further, with $G \cong Q_0 + Q_1G + Q_2G$ gave us $|G|(X)=\frac{1}{1-x-x^2}$ and the Fibonacci numbers.
Going yet one more level, we get the tribonacci numbers, which are those that follow

$T_0 = T_1 = T_2= 1$
$T_{n+3} = T_n + T_{n+1} + T_{n+2}$

i.e. 1, 1, 1, 3, 5, 9, 17, 31, …

Indeed, there’s a species $H \cong Q_0 + Q_1H + Q_2H + Q_3H$ with $|H|(X) = \frac{1}{1-x-x^2-x^3}$ , and we can show (using the same ideas) that $|H|(X) = \sum_{n\geq0} T_n x^n$ , and that

$T_n$ = |{ ways to chop {0, … , n-1} into blocks of length 1, 2, or 3}|.

Trees

Let $B \colon \mathsf S \to \mathsf F$ be the species with

B(X) = {binary rooted planar trees with leaves equipped with a bijection to X}

as in Lecture 3. Notice that

|B(n)|= n! |{binary rooted planar trees}|

since a B-structure on X is a total ordering along with a choice of binary rooted planar tree. For example, |B(5)| = 5! 5.

Here, $B\cong A_1+B\cdot B$ , i.e. a tree with X-labelled leaves is either just a root, or given by chopping X into two subsets and putting a labelled tree structure on the leftover stuff. Using this, we see that $B^2-B+X=0$ gives

$B= \frac{-1\pm\sqrt{(-1)^2-4\cdot1\cdot x}}{2\cdot1}$
$= \frac{1\pm\sqrt{1-4x}}{2}$

but since |B(0)| should be 0, not 1, we see that we want to take the root given by taking $\pm$ to be -. So write $|B|(X) = \sum_{n\geq0} \frac{|B(n)|}{n!} x^n$ . For $n>0$ ,

$|B(n)|= \frac{\mathrm{d}^n}{\mathrm{d}x^n} \left(\frac{1-\sqrt{1-4x}}{2}\right) \Bigg|_{x=0}$
$= -\frac12\frac{\mathrm{d}^n}{\mathrm{d}x^n} \big(\sqrt{1-4x}\big) \Big|_{x=0}$

and so

$|B(1)| = -\frac12\cdot\frac12\cdot(-4)\cdot(1-4x)^{-\frac12} \Big|_{x=0}$
$= -\frac12\cdot\frac12\cdot(-4) = 1$

$|B(2)| = -\frac12\cdot\frac12\cdot\left(-\frac12\right)\cdot(-4)^2\cdot(1-4x)^{-\frac32} \Big|_{x=0}$
$= -\frac12\cdot\frac12\cdot\left(-\frac12\right)\cdot(-4)^2 = 2$

$|B(3)| = -\frac12\cdot\frac12\cdot\left(-\frac12\right)\cdot\left(-\frac32\right)\cdot(-4)^3 = 12$
…
$|B(n)| = \frac{(-4)^n}{2^{n+1}}\cdot(-1)^n\cdot(2n-3)$
$= \frac{2^{2n}}{2^{n+1}}(2n-3)!!$
$= 2^{n-1}(2n-3)!!$