I’m currently teaching an informal course in category theory at Caltech. As I’m currently writing, I’ve given one lecture so far. One of the goals here is to get them up to the point where they could *begin* to read current research in applied category theory. So I hope they could pick up a paper in categorical quantum computation, categorical probability, or categorical systems theory and at least be able to say “ok, I’ve heard of the main object of study here before”. About 20 people showed up, and maybe half the people in the room were in either the Ames group (as I am) or the Burdick group. So another goal of the course is to get those people in particular up to the point where they could be my coauthors in future work, and hopefully when I leave Caltech a thread of categorical methods could be maintained. Both of these goals are somewhat ambitious, but I think it’s a worthwhile place to put some energy. In particular, as I’ve been interacting more with engineers the past few years, I’ve heard from a few people that they are looking for grad students and postdocs who know category theory, but are interest in in the applications side (also with the giant asterisk of living in or willing to move to the U.S.). The situation for ACT in the US is interesting at the moment. There never have been many professors producing ACT students, and there might be fewer now than there were ten years ago. I haven’t rigorously counted. A short term solution is to find those professors and recommend their students to people who ask. A longer term solution is to teach category theory to more people at all levels so there are generally more people in the market who have at least some basis to build on.
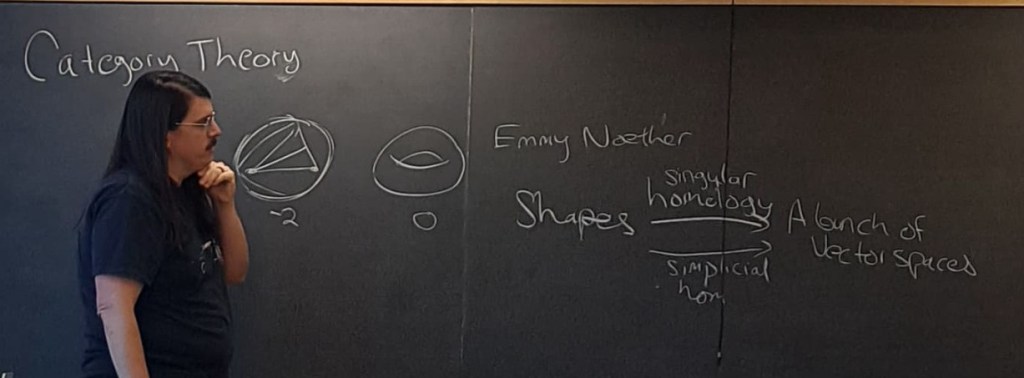
In my first lecture, I started by with a brief historical account of the origin of CT starting with Euler characteristic (you can get the gist from the picture above). Then I gave examples before even giving the formal definition. I started with the category Set, recalling things you learn about in a basic set theory class like functions, intersection, union, disjoint union, product, to look back on as we learn more category theory. I talked in slightly less detail about the category of matrices, the category of vector spaces, and the subcategory of finite dimensional vector spaces. At this point I could feel that I had spent all the goodwill they had for listening to examples without a definition. So I started writing down the definition, but I stopped after saying that you have objects and morphisms because I wanted to spend time explaining those things in all the previous examples. Then I continued the formal definition with the composition rule. At this point, a neuroscience grad student asked if I could write a short informal definition to go along with the long drawn out formal definition. I had never really thought of the definition of category as being a long one, especially compared to some of the definitions you can get into later in the subject. Next time I teach this course, I’ll start with the informal definition even before the examples. Otherwise it just sorta looks like I’m rambling about a bunch of semi-related undergrad math in a dadesque manner. The course is only one hour per week, so this is all I had time to get into, but I told myself while preparing for the class that I was going to give at least one example of a thing you can say in the language of categories. So I just quickly defined isomorphism before letting them go. I think this maybe wasn’t perfect, but that’s how these things go.
One thought on “Teaching category theory to engineers (part 1)”