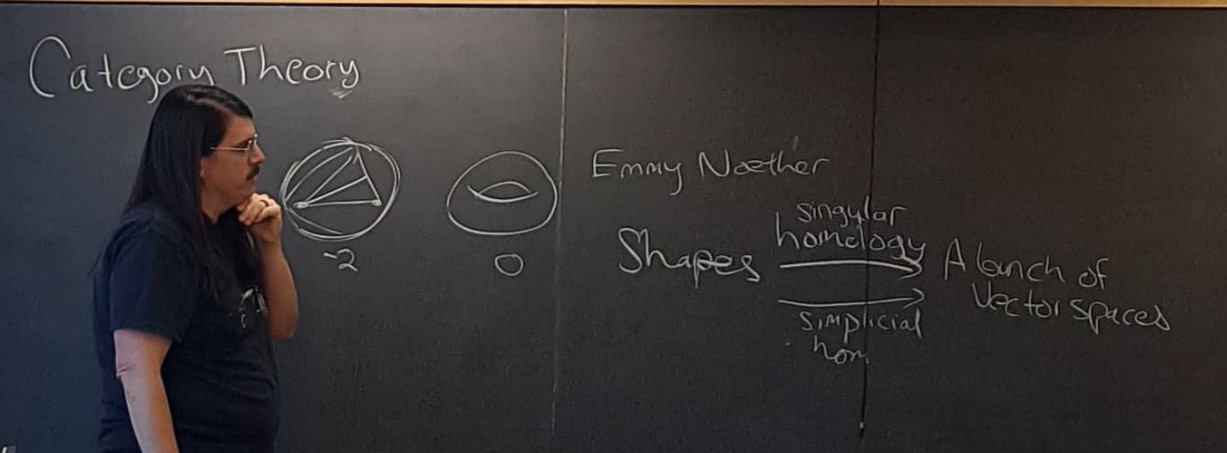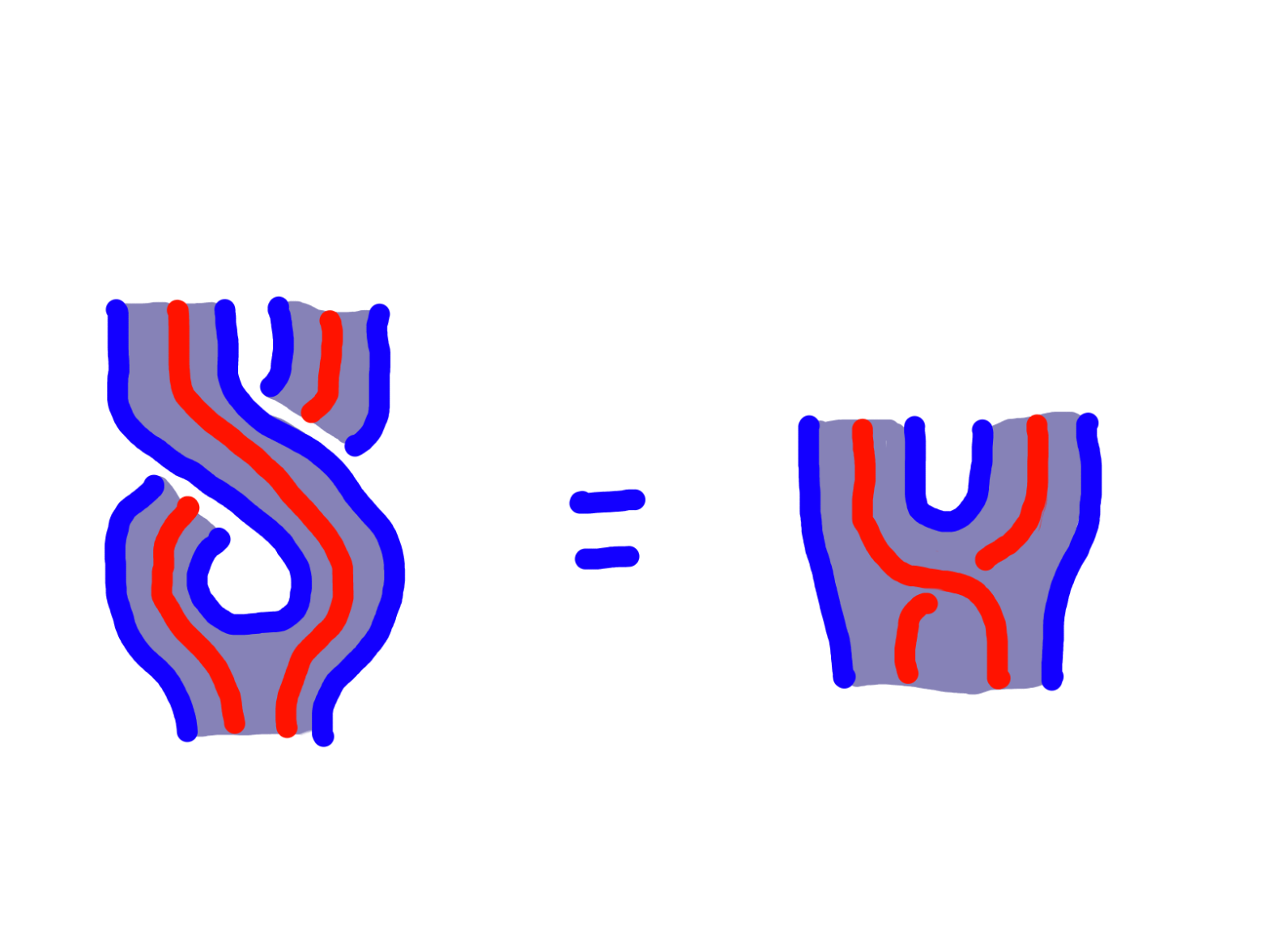I’ll start off with a clarification. My students are engineers in the sense that they are PhD students and postdoc in control theory. So they’re very well acquainted with certain sections of modern mathematics: dynamical systems, optimization, some differential geometry, but not so much abstract algebra. The experience with linear algebra is interesting, because itContinueContinue reading “Teaching category theory to engineers (part 4)”
Author Archives: Joe Moeller
Teaching category theory to engineers (part 3)
I have heard the requests to start posting lecture notes. I’ll get to it soon. These posts are my reflections on the experience of putting this course together and how the students respond. I’ve committed one of the cardinal sins of teaching category theory. I never mentioned the fact that the naming convention for categoriesContinueContinue reading “Teaching category theory to engineers (part 3)”
Teaching category theory to engineers (part 2)
Last time, I mentioned that I would have changed up how I presented the initial information. A few people couldn’t make it to the first lecture. So I offered to show up an hour early this week and essentially give the first lecture again. As you might expect, the second time around was much better!ContinueContinue reading “Teaching category theory to engineers (part 2)”
We’re building a space robot
If you want to test out new control algorithms on a piece of machinery that costs billions of dollars, it’s probably a good idea to first test them out on machinery that only costs thousands of dollars first. My colleague Pedro Roque designed a robot for this purpose. The thing on top is a graspingContinueContinue reading “We’re building a space robot”
Teaching category theory to engineers (part 1)
I’m currently teaching an informal course in category theory at Caltech. As I’m currently writing, I’ve given one lecture so far. One of the goals here is to get them up to the point where they could *begin* to read current research in applied category theory. So I hope they could pick up a paperContinueContinue reading “Teaching category theory to engineers (part 1)”
Posets inside of categories
A poset can be thought of as a category with the property that each hom-set is either empty or singleton (technically that’s a preorder, but I’ll skip that for now). There’s also a category of posets. In my work lately, I’ve actually wanted to point at an object in a category and say “this oneContinueContinue reading “Posets inside of categories”
Hawk-Dove game in Julia
Years ago, I would took a bunch of CS courses with C++ as the language of interest. One of the main projects I worked on completely outside of any course was an implementation of the Hawk-Dove game. I recently tried to find the files from this, and came up empty-handed. Instead of getting bummed thatContinueContinue reading “Hawk-Dove game in Julia”
Adjoint School 2023
Category theory has been “applied” in one sense or another since the beginning. Eilenberg himself studied automata theory. But the applied category theory community as it currently exists formally coalesced in 2018. All at once, we had the first instance of the Applied Category Theory conference, the accompanying Adjoint School, and the announcement of theContinueContinue reading “Adjoint School 2023”
Delooping, and internalization vs enrichment
Originally I was planning to write a post called something like “monoid facts everyone should know”, but I’m going easy on myself and giving you just one fact for now. If you ask someone for the definition of a monoid, there are two sorts of answers you’ll get: it’s a set equipped with an associativeContinueContinue reading “Delooping, and internalization vs enrichment”
Tube diagrams for monoidal monads
In this post, I’ll show you the diagrams I used while thinking about monoidal monads. this is building on the diagrams I show you in the first part. There, I showed you the tube-and-string diagrams for just ordinary monads, but I don’t think this is honestly better than other stringy presentations of monads. It’s probablyContinueContinue reading “Tube diagrams for monoidal monads”