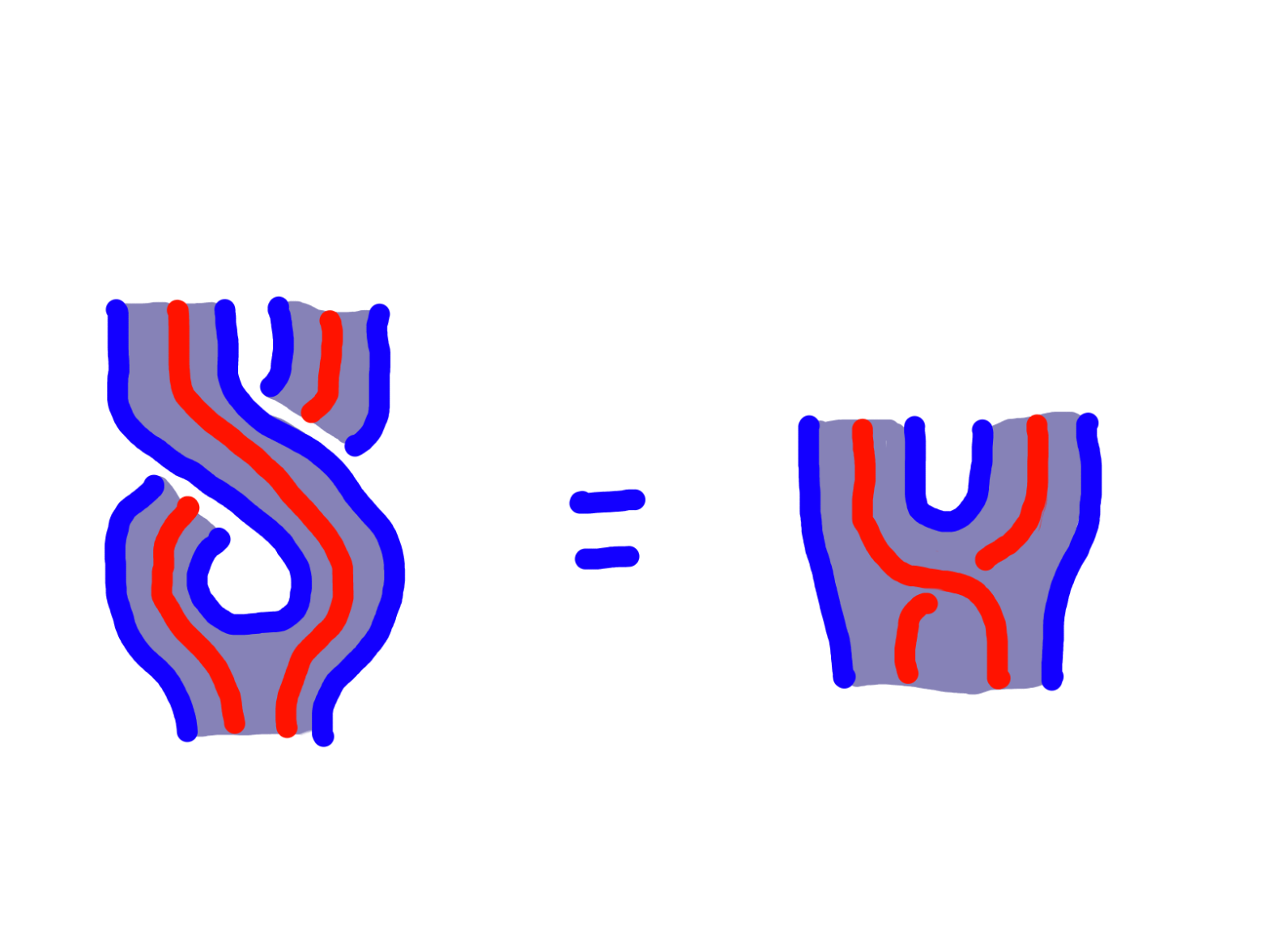Uncategorized – Joe Moeller

A boring blog post

I haven’t blogged in a while. I don’t want to spend too much time speculating why, but I’ll blame it on the pandemic. I want to get back into blogging now. I keep saying that, but I’m not doing it. I let the ads on WordPress be an excuse for a while, but now IContinueContinue reading “A boring blog post”

Tube diagrams for monoidal monads

In this post, I’ll show you the diagrams I used while thinking about monoidal monads. this is building on the diagrams I show you in the first part. There, I showed you the tube-and-string diagrams for just ordinary monads, but I don’t think this is honestly better than other stringy presentations of monads. It’s probablyContinueContinue reading “Tube diagrams for monoidal monads”

Combinatorics, Lecture 5 (10 October 2019)

Thanks to Tim Hosgood for helping me type these notes up. Previous lecture here. Fibonacci and `tribonacci’ numbers Recall: there’s a species $latex G \colon \mathsf S \to \mathsf F$ with G(X) = {ways to totally order X and chop it into blocks of length 1 or 2} For example, We saw that $latex |G|(X)ContinueContinue reading “Combinatorics, Lecture 5 (10 October 2019)”

Combinatorics, Lecture 4 (8 Oct 2019)

Lecture 3 here. Using Generating Functions We defined two binary operations on species $latex \mathsf{S} \to \mathsf{Set}$: Addition. $latex (G+H)(X)=G(X)+H(X)$; Multiplication. $latex (GH)(X) = \{(Y,g,h) \mid Y \subseteq X, g \in G(Y), h \in H (X \setminus Y)\}$. These obey $latex |G+H| = |G|+|H|$ and $latex |GH|=|G||H|$. In total, we’ll talk about five binary operationsContinueContinue reading “Combinatorics, Lecture 4 (8 Oct 2019)”

Combinatorics, Lecture 3 (3 Oct 2019)

Lecture 2 here. Thanks again to Tim Hosgood for the beautiful pictures. The category of species Last time, we looked at the relationship between species and their generating functions, a formal power series associated to a species which lets you count structures described by the species. Now we’ll take a closer look at species themselves.ContinueContinue reading “Combinatorics, Lecture 3 (3 Oct 2019)”

Combinatorics, Lecture 2 (1 Oct 2019)

In Lecture 1, we gave the idea of what a species is and saw a few examples. Now we’ll explore the idea more and see more examples. We’ll also talk about the connection to generating functions, and some operations that let us build new species from old. Thanks to Tim Hosgood for helping me outContinueContinue reading “Combinatorics, Lecture 2 (1 Oct 2019)”

How I got into my research

Due to some conversations that were happening on Twitter, I feel compelled to tell the story of how I got into my research and the role that my advisor played. Note that I went to UC Riverside for my B.S., which is also where I’m doing my PhD now. Choosing an advisor In undergrad, IContinueContinue reading “How I got into my research”

Reference List: Operads and Combinatorial Species

(1972) The Geometry of Iterated Loop Spaces – May [pdf](1973) Homotopy Invariant Algebraic Structures on Topological Spaces – Boardman, Vogt(1981) Une théorie combinatoire des séries formelles – Joyal [link](1989) The Relation between Burnside Rings and Combinatorial Species – Labelle, Yeh [link](1990) Generatingfunctionology – Wilf [link](1997) Combinatorial Species and Tree-like Structures – Bergeron, Leroux, Labelle [firstContinueContinue reading “Reference List: Operads and Combinatorial Species”

Algebraic Analysis notes Lecture 9 (30 Jan 2019)

Notes for lecture 8 Last time we showed that Sh(X;k) is an abelian category. So we’ll get: a notion of simple objectscomplexes, exactness, cohomology of complexes5-lemmasnake lemmaJordan-Holder theorem for abelian categories of finite length For $latex \phi \colon F \to G$, we saw $latex ker (\phi)_x \cong ker (\phi_x)$ and $latex cok (\phi)_x \cong cokContinueContinue reading “Algebraic Analysis notes Lecture 9 (30 Jan 2019)”