Algebraic Analysis notes Lecture 8 (28 Jan 2019)

Last time: we defined additive categories, and kernels for morphisms in additive categories.

Definition: The cokernel of a morphism $\phi$ (if it exists) is the universal object $cok \phi$ with the dual universal property:

Definition: an additive category C is abelian if
(A4) for any $\phi \colon X \to Y$ , the kernel and cokernel exist, and the natural map $\psi$ :

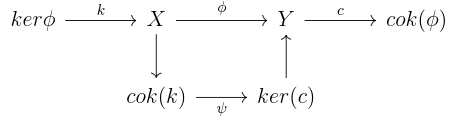
is an isomorphism.

Remark: A4 implies that if $\phi$ has $ker \phi = 0$ and $cok \phi = 0$ , then $\phi$ is an isomorphism.

Examples:

Ab, or more generally k-mod, is additive, and A4 holds because $cok(k) = X / ker\phi \cong im \phi = ker(c)$ by the first isomorphism theorem
PreSh(X;k) is abelian, as we saw last time, given $\phi \colon F \to G$ , then $ker\phi$ is given by $ker \phi (U) = ker (\phi(U) \colon F(U) \to G(U))$ , and $ker \phi$ is a presheaf which is the kernel of $\phi$ . Let $cok^{pre}(\phi)(U) = cok(\phi(U) \colon F(U) \to G(U))$ , and by similar reasoning, this is the cokernel in PreSh(X;k). Then for U open in X, reduces to the case in k-mod. Thus PreSh(X;k)

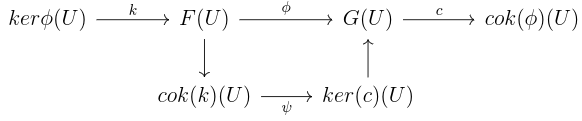
Sheaves need a little more work. If $\phi \colon F \to G$ is a map of sheaves, $cok^{pre}(\phi)$ might not be a sheaf.

Proposition: In Sh(X;k), the cokernel of $\phi \colon F \to G$ is given by $cok\phi = cok^{pre}\phi^+$ , and on stalks $(cok \phi)_x = cok(\phi_x \colon F_x \to G_x)$ .

proof: Recall that a map of sheaves is just a map of presheaves that happens to go between sheaves. Given a sheaf A, and a morphism $f \colon G \to A$ such that $f \circ \phi = 0$ , universal property of $cok^{pre}(\phi)$ in PreSh(X;k) gives a map $h \colon cok^{pre}(\phi) \to A$ . Then universal property of sheafification says that the map $h \colon cok^{pre}(\phi) \to A$ induces a map $h^+ \colon cok^{pre}(\phi)^+ \to A$ .

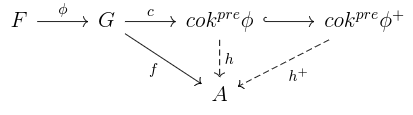
Jade Master, sitting next to me in class, pointed out that you can just invoke “left adjoints preserve colimits”.

Direct limits in k-mod are exact. So they commute with kernels and cokernels, giving $(ker \phi)_x = ker (\phi_x)$ and $(cok \phi)_x = cok (\phi_x)$ (sheafification preserves stalks).

Lemma: Let $\phi \colon F \to G$ be a map of sheaves. The following are equivalent:

$\phi$ is an isomorphism
for any U open in X, $\phi(U) \colon F(U) \to G(U)$ is an isomorphism
for any point x in X, $\phi_k \colon F_x \to G_x$ is an isomorphism

proof: (1 <=> 2) is obvious. (3 => 2) is obvious. Suppose $\phi_x$ is an isomorphism for every point x in X. We want to show that $\phi_U$ is an isomorphism for each U open in X. Fix U open in X. Let $s \in F(U)$ . If $\phi_U(s) = 0$ , then $\phi_U (s)_x = 0 = \phi_x (s_x)$ , so $s_x = 0$ for each x, so s=0, so $\phi_u$ is injective.

Let $t \in G(U)$ . For each point x in X, consider $\phi^{-1}_x (t_x) \in F_x$ . Let $U^x$ be an open neighborhood of x, and $s^x \in F(U^x)$ such that $s^x_x = \phi^{-1}_x (t_x)$ . Then $(\phi_{U^x} (s^x))_x = t_x$ , so there is a $V^x \subset U^x$ such that $\phi_{U^x} (s^x) |_{V^x} = t |_{V^x}$ .

claim: $s^x |_{V^x \cap V^y} = s^y |_{V^x \cap V^y}$ . We want this so that the $s^x$ glue to give $s \in F(U)$ . Recall that we showed $\phi_U$ is injective for all U open in X, and note

$\phi_{V^x \cap V^y} (s |_{V^x \cap V^y}) = \phi_{V^x} (s^x) |_{V^x \cap V^y}$
$= t |_{V^x \cap V^y} = \phi_{U^y} (s^y) |_{V^x \cap V^y}$
$= \phi_{V^x \cap V^y} (s^y |_{V^x \cap V^y})$

Thus there is an $s \in F(U)$ such that $s|_{U^x} = s^x$ and $\phi_U(s) |_{U^x} = \phi_{U^x} (s^x) = t|_{U^x}$ . Then by uniqueness of sections, $\phi_U(s) = t$ , so $\phi_U$ is surjective, completing the proof.

Theorem: Sh(X;k) is abelian.

Let $\phi \colon F \to G$ be a map of sheaves.

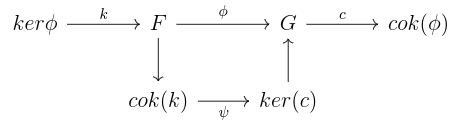
We need to show that $\psi$ is an isomorphism. It suffices to check on stalks. But $(ker(f))_x = ker(f_x)$ and $(cok(f))_x = cok(f_x)$ , so it reduces to k-mod.