Algebraic Analysis notes Lecture 10 (1 Feb 2019)

Posted byJoe MoellerPosted inAlgebraic Geometry

Notes for lecture 9

Last time: \Gamma : Sh(X; k) \to k-mod global sections functor is left exact. We’ll leave sheaves for now to look at derived categories. What do sheaves have to do with cohomology?

Poincare Lemma: Let M be a manifold. Consider the following complex of sheaves:

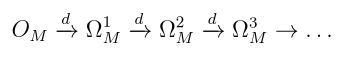
where d is the de Rham differential, and \mathcal O_M consists of smooth functions. This complex is a resolution of the constant sheaf \underline{\mathbb R}_M!

Then apply \Gamma:

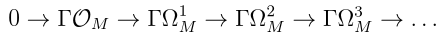
This is a chain complex of real vector spaces. The cohomology of this complex is the de Rham cohomology:

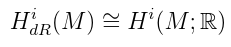
This construction is analogous to the definition/construction of Ext groups! Let X be a k-module, and given another k-module Y take a projective resolution of Y:

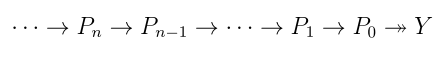
Apply Hom(X, -) to this resolution to get a complex

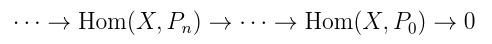
Then let Ext^i (X, Y) = H^i (\mathrm{Hom} (X, P_\bullet)).

Exercise: The k-module Ext^i (X, Y) doesn’t depend on the choice of resolution.

Ext^i and H^i_{sing} are examples of derived functors.

Category of Complexes

Definition: A complex in an abelian category is a sequence

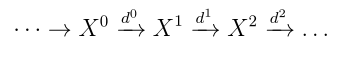
such that d^i \circ d^{i-1} = 0 for any i. A homomorphism of complexes is a collection of maps f^i : X^i \to Y^i such that all the squares commute.

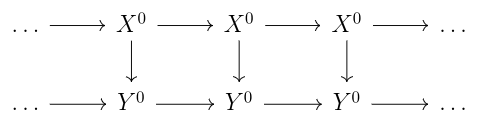
Let C(A) be the category of complexes in A. Note the kernel and cokernel are given by ker (f)^i = ker (f^i) and cok (f)^i = cok (f^i). For each i, we have a functor H^i : C(A) \to A given by X^\bullet \mapsto ker d^i / im d^{i-1}, the ith cohomology of X^\bullet.

Definition: If X^\bullet \in C(A), let X^\bullet [n] be the shifted complex X[n]^i = X^{i+n} and d_{X[n]}^i = (-1)^n d^{i+n}_X.

Why the sign? We want things to be “graded-commutative”, i.e. if s, t are homogeneous operators, then ts = (-1)^{|s||t|} st, |[n]| = n, |d|=1. Whereas f : X^\bullet \to Y^\bullet has degree 0 f[n]^i = f^{i+n}.

Note for abelian category A that A \hookrightarrow C(A) by X \mapsto (\dots \to 0 \to X \to 0 \to \dots). This makes A a full subcategory of C(A).

Definition: A homomorphism f of complexes is a quasi-isomorphism if the map f induces on cohomology H^i (X^\bullet) \to H^i(Y^\bullet) is an isomorphism.

Definition: A complex is acyclic if it is quasi-isomorphic to 0, i.e. H^i(A) = 0 for all i.

Definition: The mapping cone of f : X^\bullet \to Y^\bullet is the complex C(f) where C(f)^n = X^{n+1} \oplus Y^n and d^n (x, y) = (-d_X^{n+1} (x), f^{n+1} (x + d_Y^n (y)).

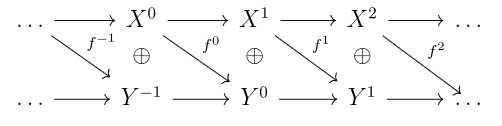
Check that this is a complex.

Exercises:

  • C(f) is functorial.
  • there is a short exact sequence 0 \to B^\bullet \xrightarrow{i} C(f) \xrightarrow{p} A[1] \to 0
  • Let K = ker(f), Q = cok(f). Then
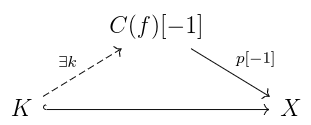
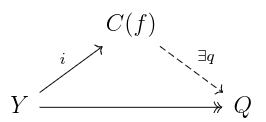
  • If f is injective (resp. surjective) then q : C(f) \to Q (resp. k[1] : K[1] \to C(f)) is a quasi-isomorphism.
  • If f is an isomorphism, then C(f) is acyclic.
  • For any i, the short exact sequence above induces exact H^i(Y) \to H^i(C(f)) \to H^{i+1}(X)

Definition: A map f : X^\bullet \to Y^\bullet is null-homotopic if there is a map s^i : X^i \to Y^{i-1} such that f^i = d_Y^{i-2} s^i + s^{i+1} d_X^i for each i.

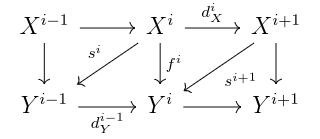
We say f and g are homotopic, and write f~g, if f-g is null-homotopic.

Note if f~0, then h \circ f \sim 0 and f \circ g \sim 0 for any h, g.

Definition: The homotopy category K(A) of an abelian category A is the category with complexes of A for objects, and homotopy classes of complex homomorphisms for morphisms \mathrm{Hom}_{K(A)} (X^\bullet, Y^\bullet) = \mathrm{Hom}_{C(A)} (X^\bullet, Y^\bullet) / \sim.

Notes for Lecture 11

Published by Joe Moeller

Mathematician

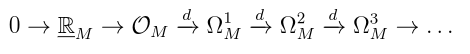
2 thoughts on “Algebraic Analysis notes Lecture 10 (1 Feb 2019)”

  1. Pingback: Algebraic Analysis notes Lecture 9 (30 Jan 2019) – Joe Moeller
  2. Pingback: Algebraic Analysis notes Lecture 11 (4 Feb 2019) – Joe Moeller

Leave a comment