Algebraic Analysis notes Lecture 11 (4 Feb 2019)

Notes for lecture 10

Last time: for an abelian category A, C(A) is the category of complexes in A. Say $f, g \in \mathrm{Hom}_{C(A)} (X, Y)$ are homotopic, f~g, if there are maps $s^i : X^i \to Y^i$ such that $f^i -g^i = d_Y s + sd_X$ .

Definition The homotopy category K(A) of A is the category with objects complexes of A, and morphisms are homotopy classes of morphisms of complexes. The motivation for this is from algebraic topology, where there is a homotopy category of topological spaces, hTop, where the objects are topological spaces and the morphisms are homotopy classes of continuous maps.

Example Singular cochains gives a functor $hTop \to K(\mathbb Z-mod)$ .

Let $Hom^n (X^\bullet, Y^\bullet) = \prod_{\mathbb Z} Hom(X^i, Y^i)$ . Note that the squares formed by an element of this set do not necessarily have to commute. Then we get a complex $Hom^\bullet (X^\bullet, Y^\bullet)$ . Let $d^n (( \phi^i)_{i \in \mathbb Z}) = (d_Y^{i+n} \phi^i - (-1)^n \phi^{i+1} d_X^i$ . Note that for $\phi \in Hom^0 (X, Y)$ , $\phi$ is in the kernel of $d^0$ iff $d_Y \phi = \phi d_X$ iff f~0. Thus $Hom_{K(A)} ( X^\bullet, Y^\bullet) \cong H^0 (Hom^\bullet (X^\bullet, Y^\bullet)$ .

We also defined the mapping cone $C(f) \in C(A)$ for a map $f : X^\bullet \to Y^\bullet$ .

Proposition/Exercise For a map of complexes $f : X^\bullet \to Y^\bullet$ in A, the following are equivalent:

f~0
f factors through the canonical map $i : X \to C(1_X)$
f factors through the canonical map $p [-1] : C(1_Y) [-1] \to Y$
the sequence $0 \to Y \to C(f) \to X [1] \to 0$ splits

Corollary If $f,g : X^\bullet \to Y^\bullet$ and f~g, then $f^* = g^* : H^i(X) \to H^i(Y)$ for each i. Hence, we get well-defined cohomology functors, $K(A) \to A$ where $X \mapsto H^i(X)$ .

proof If f~0, then f factors through $C(1_X)$ which is acyclic!

Corollary Every homotopy equivalence (i.e. isomorphism in K(A)) is a quasi-isomorphism.

Note that K(A) (nor the derived category D(A), as we will see) is an abelian category! It is a triangulated category.

Lemma Given $f : X^\bullet \to Y^\bullet$ a map of complexes in A, we get the sequence

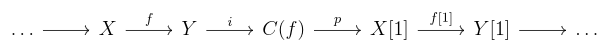
The composite of any two consecutive maps is zero in K(A).

proof The composite of $Y \to C(f) \to X[1]$ is zero on the nose. For $X \to Y \to C(f)$ , then

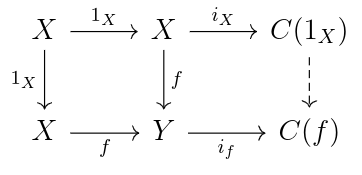
So $i \circ f$ factors through $i_X$ , so $i \circ f ~0$ . Similar for $C(f) \to A[1] \to B[1]$ .

Definition A triangle in an additive category with a shift funcor [1] is a sequence $A \xrightarrow{f} B \xrightarrow{g} C \xrightarrow{h} A[1] \to \dots$ , such that is the long sequence, any two consecutive maps compose to zero.

So $X \to Y \to C(f) \to A[1]$ is a triangle in K(A).

A morphism of triangles is a commutative diagram:

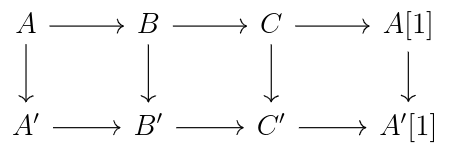
In K(A), a standard triangle is one of the form $X \xrightarrow{f} Y \to C(f) \to X[1]$ . An exact triangle in K(A) is one that is isomorphic to a standard triangle.

Proposition Exact triangles satisfy:

for any map $f : X \to Y$ there is an exact triangle $X \to Y \to Z \to X[1]$ and $X \xrightarrow{1_X} X \to 0 \to X[1]$ is an exact triangle
If $X \to Y \to Z \to X[1]$ is an exact triangle, so are its rotations $Y \to Z \to X[1] \to Y[1]$ and $Z[-1] \to X \to Y \to Z$
Direct sum of exact triangles is exact
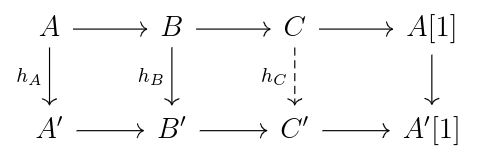
Given two exact triangles $A \to B \to C \to A[1]$ , and $A' \to B' \to C' \to A'[1]$ , and morphisms $h_A :A \to A'$ and $h_B : B \to B'$ such that the square commutes, then there exists a map $h_c : C \to C'$ making this collection of maps a map of triangles